These tutorials have been some of the most heavily requested lessons on the PyImageSearch blog. I’m super excited to get them underway — and I’m sure you are too.
However, before we start learning how to measure the size (and not to mention, the distance between) objects in images, we first need to talk about something…
A little over a year ago, I wrote one my favorite tutorials on the PyImageSearch blog: How to build a kick-ass mobile document scanner in just 5 minutes. Even though this tutorial is over a year old, its still one of the most popular blog posts on PyImageSearch.
Building our mobile document scanner was predicated on our ability to apply a 4 point cv2.getPerspectiveTransform with OpenCV, enabling us to obtain a top-down, birds-eye-view of our document.
However. Our perspective transform has a deadly flaw that makes it unsuitable for use in production environments.
You see, there are cases where the pre-processing step of arranging our four points in top-left, top-right, bottom-right, and bottom-left order can return incorrect results!
To learn more about this bug, and how to squash it, keep reading.
Ordering coordinates clockwise with Python and OpenCV
The goal of this blog post is two-fold:
- The primary purpose is to learn how to arrange the (x, y)-coordinates associated with a rotated bounding box in top-left, top-right, bottom-right, and bottom-left order. Organizing bounding box coordinates in such an order is a prerequisite to performing operations such as perspective transforms or matching corners of objects (such as when we compute the distance between objects).
- The secondary purpose is to address a subtle, hard-to-find bug in the
order_pointsmethod of the imutils package. By resolving this bug, ourorder_pointsfunction will no longer be susceptible to a debilitating bug.
All that said, let’s get this blog post started by reviewing the original, flawed method at ordering our bounding box coordinates in clockwise order.
The original (flawed) method
Before we can learn how to arrange a set of bounding box coordinates in (1) clockwise order and more specifically, (2) a top-left, top-right, bottom-right, and bottom-left order, we should first review the order_points method detailed in the original 4 point getPerspectiveTransform blog post.
I have renamed the (flawed) order_points method to order_points_old so we can compare our original and updated methods. To get started, open up a new file and name it order_coordinates.py :
# import the necessary packages from __future__ import print_function from imutils import perspective from imutils import contours import numpy as np import argparse import imutils import cv2 def order_points_old(pts): # initialize a list of coordinates that will be ordered # such that the first entry in the list is the top-left, # the second entry is the top-right, the third is the # bottom-right, and the fourth is the bottom-left rect = np.zeros((4, 2), dtype="float32") # the top-left point will have the smallest sum, whereas # the bottom-right point will have the largest sum s = pts.sum(axis=1) rect[0] = pts[np.argmin(s)] rect[2] = pts[np.argmax(s)] # now, compute the difference between the points, the # top-right point will have the smallest difference, # whereas the bottom-left will have the largest difference diff = np.diff(pts, axis=1) rect[1] = pts[np.argmin(diff)] rect[3] = pts[np.argmax(diff)] # return the ordered coordinates return rect
Lines 2-8 handle importing our required Python packages for this example. We’ll be using the imutils package later in this blog post, so if you don’t already have it installed, be sure to install it via pip :
$ pip install imutils
Otherwise, if you do have imutils installed, you should upgrade to the latest version (which has the updated order_points implementation):
$ pip install --upgrade imutils
Line 10 defines our order_points_old function. This method requires only a single argument, the set of points that we are going to arrange in top-left, top-right, bottom-right, and bottom-left order; although, as we’ll see, this method has some flaws.
We start on Line 15 by defining a NumPy array with shape (4, 2) which will be used to store our set of four (x, y)-coordinates.
Given these pts , we add the x and y values together, followed by finding the smallest and largest sums (Lines 19-21). These values give us our top-left and bottom-right coordinates, respectively.
We then take the difference between the x and y values, where the top-right point will have the smallest difference and the bottom-left will have the largest distance (Lines 26-28).
Finally, Line 31 returns our ordered (x, y)-coordinates to our calling function.
So all that said, can you spot the flaw in our logic?
I’ll give you a hint:
What happens when the sum or difference of the two points is the same?
In short, tragedy.
If either the sum array s or the difference array diff have the same values, we are at risk of choosing the incorrect index, which causes a cascade affect on our ordering.
Selecting the wrong index implies that we chose the incorrect point from our pts list. And if we take the incorrect point from pts , then our clockwise top-left, top-right, bottom-right, bottom-left ordering will be be destroyed.
So how can we address this problem and ensure that it doesn’t happen?
To handle this problem, we need to devise a better order_points function using more sound mathematic principles. And that’s exactly what we’ll cover in the next section.
A better method to order coordinates clockwise with OpenCV and Python
Now that we have looked at a flawed version of our order_points function, let’s review an updated, correct implementation.
The implementation of the order_points function we are about to review can be found in the imutils package; specifically, in the perspective.py file. I’ve included the exact implementation in this blog post as a matter of completeness:
# import the necessary packages from scipy.spatial import distance as dist import numpy as np import cv2 def order_points(pts): # sort the points based on their x-coordinates xSorted = pts[np.argsort(pts[:, 0]), :] # grab the left-most and right-most points from the sorted # x-roodinate points leftMost = xSorted[:2, :] rightMost = xSorted[2:, :] # now, sort the left-most coordinates according to their # y-coordinates so we can grab the top-left and bottom-left # points, respectively leftMost = leftMost[np.argsort(leftMost[:, 1]), :] (tl, bl) = leftMost # now that we have the top-left coordinate, use it as an # anchor to calculate the Euclidean distance between the # top-left and right-most points; by the Pythagorean # theorem, the point with the largest distance will be # our bottom-right point D = dist.cdist(tl[np.newaxis], rightMost, "euclidean")[0] (br, tr) = rightMost[np.argsort(D)[::-1], :] # return the coordinates in top-left, top-right, # bottom-right, and bottom-left order return np.array([tl, tr, br, bl], dtype="float32")
Again, we start off on Lines 2-4 by importing our required Python packages. We then define our order_points function on Line 6 which requires only a single parameter — the list of pts that we want to order.
Line 8 then sorts these pts based on their x-values. Given the sorted xSorted list, we apply array slicing to grab the two left-most points along with the two right-most points (Lines 12 and 13).
The leftMost points will thus correspond to the top-left and bottom-left points while rightMost will be our top-right and bottom-right points — the trick is to figure out which is which.
Luckily, this isn’t too challenging.
If we sort our leftMost points according to their y-value, we can derive the top-left and bottom-left points, respectively (Lines 18 and 19).
Then, to determine the bottom-right and bottom-left points, we can apply a bit of geometry.
Using the top-left point as an anchor, we can apply the Pythagorean theorem and compute the Euclidean distance between the top-left and rightMost points. By the definition of a triangle, the hypotenuse will be the largest side of a right-angled triangle.
Thus, by taking the top-left point as our anchor, the bottom-right point will have the largest Euclidean distance, allowing us to extract the bottom-right and top-right points (Lines 26 and 27).
Finally, Line 31 returns a NumPy array representing our ordered bounding box coordinates in top-left, top-right, bottom-right, and bottom-left order.
Testing our coordinate ordering implementations
Now that we have both the original and updated versions of order_points , let’s continue the implementation of our order_coordinates.py script and give them both a try:
# import the necessary packages
from __future__ import print_function
from imutils import perspective
from imutils import contours
import numpy as np
import argparse
import imutils
import cv2
def order_points_old(pts):
# initialize a list of coordinates that will be ordered
# such that the first entry in the list is the top-left,
# the second entry is the top-right, the third is the
# bottom-right, and the fourth is the bottom-left
rect = np.zeros((4, 2), dtype="float32")
# the top-left point will have the smallest sum, whereas
# the bottom-right point will have the largest sum
s = pts.sum(axis=1)
rect[0] = pts[np.argmin(s)]
rect[2] = pts[np.argmax(s)]
# now, compute the difference between the points, the
# top-right point will have the smallest difference,
# whereas the bottom-left will have the largest difference
diff = np.diff(pts, axis=1)
rect[1] = pts[np.argmin(diff)]
rect[3] = pts[np.argmax(diff)]
# return the ordered coordinates
return rect
# construct the argument parse and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-n", "--new", type=int, default=-1,
help="whether or not the new order points should should be used")
args = vars(ap.parse_args())
# load our input image, convert it to grayscale, and blur it slightly
image = cv2.imread("example.png")
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
gray = cv2.GaussianBlur(gray, (7, 7), 0)
# perform edge detection, then perform a dilation + erosion to
# close gaps in between object edges
edged = cv2.Canny(gray, 50, 100)
edged = cv2.dilate(edged, None, iterations=1)
edged = cv2.erode(edged, None, iterations=1)
Lines 33-37 handle parsing our command line arguments. We only need a single argument, --new , which is used to indicate whether or not the new or the original order_points function should be used. We’ll default to using the original implementation.
From there, we load example.png from disk and perform a bit of pre-processing by converting the image to grayscale and smoothing it with a Gaussian filter.
We continue to process our image by applying the Canny edge detector, followed by a dilation + erosion to close any gaps between outlines in the edge map.
After performing the edge detection process, our image should look like this:
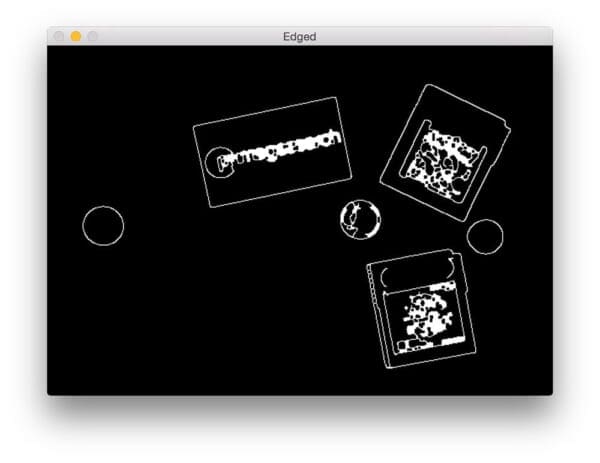
As you can see, we have been able to determine the outlines/contours of the objects in the image.
Now that we have the outlines of the edge map, we can apply the cv2.findContours function to actually extract the outlines of the objects:
# find contours in the edge map cnts = cv2.findContours(edged.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE) cnts = imutils.grab_contours(cnts) # sort the contours from left-to-right and initialize the bounding box # point colors (cnts, _) = contours.sort_contours(cnts) colors = ((0, 0, 255), (240, 0, 159), (255, 0, 0), (255, 255, 0))
We then sort the object contours from left-to-right, which isn’t a requirement, but makes it easier to view the output of our script.
The next step is to loop over each of the contours individually:
# loop over the contours individually
for (i, c) in enumerate(cnts):
# if the contour is not sufficiently large, ignore it
if cv2.contourArea(c) < 100:
continue
# compute the rotated bounding box of the contour, then
# draw the contours
box = cv2.minAreaRect(c)
box = cv2.cv.BoxPoints(box) if imutils.is_cv2() else cv2.boxPoints(box)
box = np.array(box, dtype="int")
cv2.drawContours(image, [box], -1, (0, 255, 0), 2)
# show the original coordinates
print("Object #{}:".format(i + 1))
print(box)
Line 61 starts looping over our contours. If a contour is not sufficiently large (due to “noise” in the edge detection process), we discard the contour region (Lines 63 and 64).
Otherwise, Lines 68-71 handle computing the rotated bounding box of the contour (taking care to use cv2.cv.BoxPoints [if we are using OpenCV 2.4] or cv2.boxPoints [if we are using OpenCV 3]) and drawing the contour on the image .
We’ll also print the original rotated bounding box so we can compare the results after we order the coordinates.
We are now ready to order our bounding box coordinates in a clockwise arrangement:
# order the points in the contour such that they appear
# in top-left, top-right, bottom-right, and bottom-left
# order, then draw the outline of the rotated bounding
# box
rect = order_points_old(box)
# check to see if the new method should be used for
# ordering the coordinates
if args["new"] > 0:
rect = perspective.order_points(box)
# show the re-ordered coordinates
print(rect.astype("int"))
print("")
Line 81 applies the original (i.e., flawed) order_points_old function to arrange our bounding box coordinates in top-left, top-right, bottom-right, and bottom-left order.
If the --new 1 flag has been passed to our script, then we’ll apply our updated order_points function (Lines 85 and 86).
Just like we printed the original bounding box to our console, we’ll also print the ordered points so we can ensure our function is working properly.
Finally, we can visualize our results:
# loop over the original points and draw them
for ((x, y), color) in zip(rect, colors):
cv2.circle(image, (int(x), int(y)), 5, color, -1)
# draw the object num at the top-left corner
cv2.putText(image, "Object #{}".format(i + 1),
(int(rect[0][0] - 15), int(rect[0][1] - 15)),
cv2.FONT_HERSHEY_SIMPLEX, 0.55, (255, 255, 255), 2)
# show the image
cv2.imshow("Image", image)
cv2.waitKey(0)
We start looping over our (hopefully) ordered coordinates on Line 93 and draw them on our image .
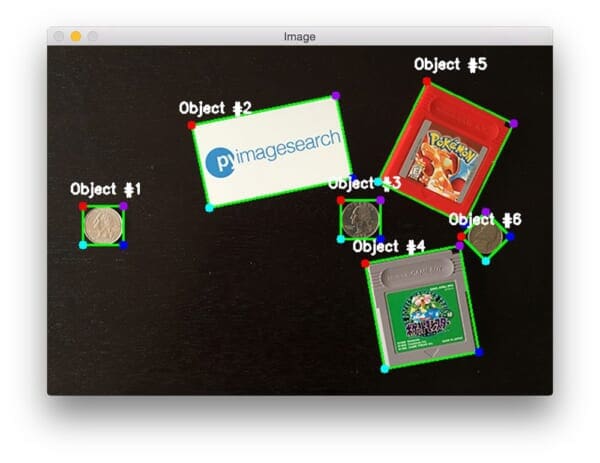
According to the colors list, the top-left point should be red, the top-right point purple, the bottom-right point blue, and finally, the bottom-left point teal.
Lastly, Lines 97-103 draw the object number on our image and display the output result.
To execute our script using the original, flawed implementation, just issue the following command:
$ python order_coordinates.py

As we can see, our output is anticipated with the points ordered clockwise in a top-left, top-right, bottom-right, and bottom-left arrangement — except for Object #6!
Note: Take a look at the output circles — notice how there isn’t a blue one?
Looking at our terminal output for Object #6, we can see why:

Taking the sum of these coordinates we end up with:
- 520 + 255 = 775
- 491 + 226 = 717
- 520 + 197 = 717
- 549 + 226 = 775
While the difference gives us:
- 520 – 255 = 265
- 491 – 226 = 265
- 520 – 197 = 323
- 549 – 226 = 323
As you can see, we end up with duplicate values!
And since there are duplicate values, the argmin() and argmax() functions don’t work as we expect them to, giving us an incorrect set of “ordered” coordinates.
To resolve this issue, we can use our updated order_points function in the imutils package. We can verify that our updated function is working properly by issuing the following command:
$ python order_coordinates.py --new 1
This time, all of our points are ordered correctly, including Object #6:

When utilizing perspective transforms (or any other project that requires ordered coordinates), make sure you use our updated implementation!
What's next? We recommend PyImageSearch University.
84 total classes • 114+ hours of on-demand code walkthrough videos • Last updated: February 2024
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you'll find:
- ✓ 84 courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 84 Certificates of Completion
- ✓ 114+ hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 536+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Summary
In this blog post, we started a three part series on calculating the size of objects in images and measuring the distance between objects. To accomplish these goals, we’ll need to order the 4 points associated with the rotated bounding box of each object.
We’ve already implemented such a function in a previous blog post; however, as we discovered, this implementation has a fatal flaw — it can return the wrong coordinates under very specific situations.
To resolve this problem, we defined a new, updated order_points function and placed it in the imutils package. This implementation ensures that our points are always ordered correctly.
Now that we can order our (x, y)-coordinates in a reliable manner, we can move on to measuring the size of objects in an image, which is exactly what I’ll be discussing in our next blog post.
Be sure to signup for the PyImageSearch Newsletter by entering your email address in the form below — you won’t want to miss this series of posts!

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!

