I’m going to start today’s blog post by asking a series of questions which will then be addressed later in the tutorial:
- What are image convolutions?
- What do they do?
- Why do we use them?
- How do we apply them?
- And what role do convolutions play in deep learning?

The word “convolution” sounds like a fancy, complicated term — but it’s really not. In fact, if you’ve ever worked with computer vision, image processing, or OpenCV before, you’ve already applied convolutions, whether you realize it or not!
Ever apply blurring or smoothing? Yep, that’s a convolution.
What about edge detection? Yup, convolution.
Have you opened Photoshop or GIMP to sharpen an image? You guessed it — convolution.
Convolutions are one of the most critical, fundamental building-blocks in computer vision and image processing. But the term itself tends to scare people off — in fact, on the the surface, the word even appears to have a negative connotation.
Trust me, convolutions are anything but scary. They’re actually quite easy to understand.
In reality, an (image) convolution is simply an element-wise multiplication of two matrices followed by a sum.
Seriously. That’s it. You just learned what convolution is:
- Take two matrices (which both have the same dimensions).
- Multiply them, element-by-element (i.e., not the dot-product, just a simple multiplication).
- Sum the elements together.
To understand more about convolutions, why we use them, how to apply them, and the overall role they play in deep learning + image classification, be sure to keep reading this post.
Convolutions with OpenCV and Python
Think of it this way — an image is just a multi-dimensional matrix. Our image has a width (# of columns) and a height (# of rows), just like a matrix.
But unlike the traditional matrices you may have worked with back in grade school, images also have a depth to them — the number of channels in the image. For a standard RGB image, we have a depth of 3 — one channel for each of the Red, Green, and Blue channels, respectively.
Given this knowledge, we can think of an image as a big matrix and kernel or convolutional matrix as a tiny matrix that is used for blurring, sharpening, edge detection, and other image processing functions.
Essentially, this tiny kernel sits on top of the big image and slides from left-to-right and top-to-bottom, applying a mathematical operation (i.e., a convolution) at each (x, y)-coordinate of the original image.
It’s normal to hand-define kernels to obtain various image processing functions. In fact, you might already be familiar with blurring (average smoothing, Gaussian smoothing, median smoothing, etc.), edge detection (Laplacian, Sobel, Scharr, Prewitt, etc.), and sharpening — all of these operations are forms of hand-defined kernels that are specifically designed to perform a particular function.
So that raises the question, is there a way to automatically learn these types of filters? And even use these filters for image classification and object detection?
You bet there is.
But before we get there, we need to understand kernels and convolutions a bit more.
Kernels
Again, let’s think of an image as a big matrix and a kernel as tiny matrix (at least in respect to the original “big matrix” image):
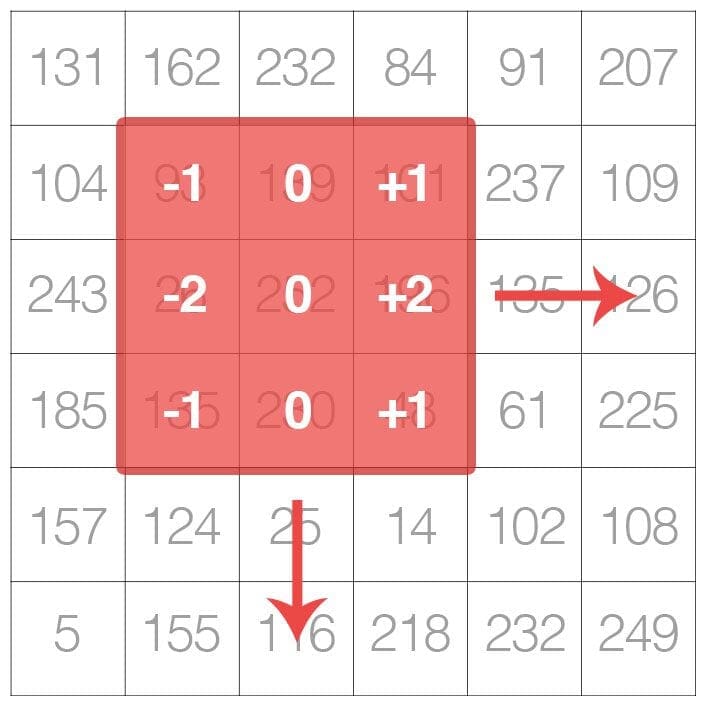
As the figure above demonstrates, we are sliding the kernel from left-to-right and top-to-bottom along the original image.
At each (x, y)-coordinate of the original image, we stop and examine the neighborhood of pixels located at the center of the image kernel. We then take this neighborhood of pixels, convolve them with the kernel, and obtain a single output value. This output value is then stored in the output image at the same (x, y)-coordinates as the center of the kernel.
If this sounds confusing, no worries, we’ll be reviewing an example in the “Understanding Image Convolutions” section later in this blog post.
But before we dive into an example, let’s first take a look at what a kernel looks like:
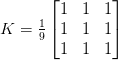
Above we have defined a square 3 x 3 kernel (any guesses on what this kernel is used for?)
Kernels can be an arbitrary size of M x N pixels, provided that both M and N are odd integers.
Note: Most kernels you’ll typically see are actually square N x N matrices.
We use an odd kernel size to ensure there is a valid integer (x, y)-coordinate at the center of the image:
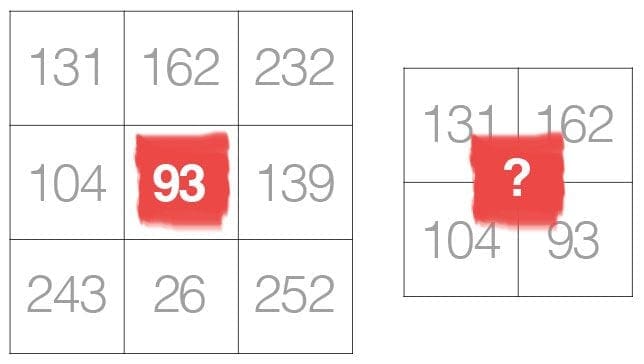
On the left, we have a 3 x 3 matrix. The center of the matrix is obviously located at x=1, y=1 where the top-left corner of the matrix is used as the origin and our coordinates are zero-indexed.
But on the right, we have a 2 x 2 matrix. The center of this matrix would be located at x=0.5, y=0.5. But as we know, without applying interpolation, there is no such thing as pixel location (0.5, 0.5) — our pixel coordinates must be integers! This reasoning is exactly why we use odd kernel sizes — to always ensure there is a valid (x, y)-coordinate at the center of the kernel.
Understanding Image Convolutions
Now that we have discussed the basics of kernels, let’s talk about a mathematical term called convolution.
In image processing, a convolution requires three components:
- An input image.
- A kernel matrix that we are going to apply to the input image.
- An output image to store the output of the input image convolved with the kernel.
Convolution itself is actually very easy. All we need to do is:
- Select an (x, y)-coordinate from the original image.
- Place the center of the kernel at this (x, y)-coordinate.
- Take the element-wise multiplication of the input image region and the kernel, then sum up the values of these multiplication operations into a single value. The sum of these multiplications is called the kernel output.
- Use the same (x, y)-coordinates from Step #1, but this time, store the kernel output in the same (x, y)-location as the output image.
Below you can find an example of convolving (denoted mathematically as the “*” operator) a 3 x 3 region of an image with a 3 x 3 kernel used for blurring:
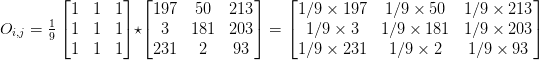
Therefore,
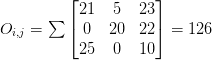
After applying this convolution, we would set the pixel located at the coordinate (i, j) of the output image O to O_i,j = 126.
That’s all there is to it!
Convolution is simply the sum of element-wise matrix multiplication between the kernel and neighborhood that the kernel covers of the input image.
Implementing Convolutions with OpenCV and Python
That was fun discussing kernels and convolutions — but now let’s move on to looking at some actual code to ensure you understand how kernels and convolutions are implemented. This source code will also help you understand how to apply convolutions to images.
Open up a new file, name it convolutions.py , and let’s get to work:
# import the necessary packages from skimage.exposure import rescale_intensity import numpy as np import argparse import cv2
We start on Lines 2-5 by importing our required Python packages. You should already have NumPy and OpenCV installed on your system, but you might not have scikit-image installed. To install scikit-image, just use pip :
$ pip install -U scikit-image
Next, we can start defining our custom convolve method:
def convolve(image, kernel): # grab the spatial dimensions of the image, along with # the spatial dimensions of the kernel (iH, iW) = image.shape[:2] (kH, kW) = kernel.shape[:2] # allocate memory for the output image, taking care to # "pad" the borders of the input image so the spatial # size (i.e., width and height) are not reduced pad = (kW - 1) // 2 image = cv2.copyMakeBorder(image, pad, pad, pad, pad, cv2.BORDER_REPLICATE) output = np.zeros((iH, iW), dtype="float32")
The convolve function requires two parameters: the (grayscale) image that we want to convolve with the kernel .
Given both our image and kernel (which we presume to be NumPy arrays), we then determine the spatial dimensions (i.e., width and height) of each (Lines 10 and 11).
Before we continue, it’s important to understand that the process of “sliding” a convolutional matrix across an image, applying the convolution, and then storing the output will actually decrease the spatial dimensions of our output image.
Why is this?
Recall that we “center” our computation around the center (x, y)-coordinate of the input image that the kernel is currently positioned over. This implies there is no such thing as “center” pixels for pixels that fall along the border of the image. The decrease in spatial dimension is simply a side effect of applying convolutions to images. Sometimes this effect is desirable and other times its not, it simply depends on your application.
However, in most cases, we want our output image to have the same dimensions as our input image. To ensure this, we apply padding (Lines 16-19). Here we are simply replicating the pixels along the border of the image, such that the output image will match the dimensions of the input image.
Other padding methods exist, including zero padding (filling the borders with zeros — very common when building Convolutional Neural Networks) and wrap around (where the border pixels are determined by examining the opposite end of the image). In most cases, you’ll see either replicate or zero padding.
We are now ready to apply the actual convolution to our image:
# loop over the input image, "sliding" the kernel across # each (x, y)-coordinate from left-to-right and top to # bottom for y in np.arange(pad, iH + pad): for x in np.arange(pad, iW + pad): # extract the ROI of the image by extracting the # *center* region of the current (x, y)-coordinates # dimensions roi = image[y - pad:y + pad + 1, x - pad:x + pad + 1] # perform the actual convolution by taking the # element-wise multiplicate between the ROI and # the kernel, then summing the matrix k = (roi * kernel).sum() # store the convolved value in the output (x,y)- # coordinate of the output image output[y - pad, x - pad] = k
Lines 24 and 25 loop over our image , “sliding” the kernel from left-to-right and top-to-bottom 1 pixel at a time.
Line 29 extracts the Region of Interest (ROI) from the image using NumPy array slicing. The roi will be centered around the current (x, y)-coordinates of the image . The roi will also have the same size as our kernel , which is critical for the next step.
Convolution is performed on Line 34 by taking the element-wise multiplication between the roi and kernel , followed by summing the entries in the matrix.
The output value k is then stored in the output array at the same (x, y)-coordinates (relative to the input image).
We can now finish up our convolve method:
# rescale the output image to be in the range [0, 255]
output = rescale_intensity(output, in_range=(0, 255))
output = (output * 255).astype("uint8")
# return the output image
return output
When working with images, we typically deal with pixel values falling in the range [0, 255]. However, when applying convolutions, we can easily obtain values that fall outside this range.
In order to bring our output image back into the range [0, 255], we apply the rescale_intensity function of scikit-image (Line 41). We also convert our image back to an unsigned 8-bit integer data type on Line 42 (previously, the output image was a floating point type in order to handle pixel values outside the range [0, 255]).
Finally, the output image is returned to the calling function on Line 45.
Now that we’ve defined our convolve function, let’s move on to the driver portion of the script. This section of our program will handle parsing command line arguments, defining a series of kernels we are going to apply to our image, and then displaying the output results:
# construct the argument parse and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-i", "--image", required=True,
help="path to the input image")
args = vars(ap.parse_args())
# construct average blurring kernels used to smooth an image
smallBlur = np.ones((7, 7), dtype="float") * (1.0 / (7 * 7))
largeBlur = np.ones((21, 21), dtype="float") * (1.0 / (21 * 21))
# construct a sharpening filter
sharpen = np.array((
[0, -1, 0],
[-1, 5, -1],
[0, -1, 0]), dtype="int")
Lines 48-51 handle parsing our command line arguments. We only need a single argument here, --image , which is the path to our input path.
We then move on to Lines 54 and 55 which define a 7 x 7 kernel and a 21 x 21 kernel used to blur/smooth an image. The larger the kernel is, the more the image will be blurred. Examining this kernel, you can see that the output of applying the kernel to an ROI will simply be the average of the input region.
We define a sharpening kernel on Lines 58-61, used to enhance line structures and other details of an image. Explaining each of these kernels in detail is outside the scope of this tutorial, so if you’re interested in learning more about kernel construction, I would suggest starting here and then playing around with the excellent kernel visualization tool on Setosa.io.
Let’s define a few more kernels:
# construct the Laplacian kernel used to detect edge-like # regions of an image laplacian = np.array(( [0, 1, 0], [1, -4, 1], [0, 1, 0]), dtype="int") # construct the Sobel x-axis kernel sobelX = np.array(( [-1, 0, 1], [-2, 0, 2], [-1, 0, 1]), dtype="int") # construct the Sobel y-axis kernel sobelY = np.array(( [-1, -2, -1], [0, 0, 0], [1, 2, 1]), dtype="int")
Lines 65-68 define a Laplacian operator that can be used as a form of edge detection.
Note: The Laplacian is also very useful for detecting blur in images.
Finally, we’ll define two Sobel filters on Lines 71-80. The first (Lines 71-74) is used to detect vertical changes in the gradient of the image. Similarly, Lines 77-80 constructs a filter used to detect horizontal changes in the gradient.
Given all these kernels, we lump them together into a set of tuples called a “kernel bank”:
# construct the kernel bank, a list of kernels we're going
# to apply using both our custom `convole` function and
# OpenCV's `filter2D` function
kernelBank = (
("small_blur", smallBlur),
("large_blur", largeBlur),
("sharpen", sharpen),
("laplacian", laplacian),
("sobel_x", sobelX),
("sobel_y", sobelY)
)
Finally, we are ready to apply our kernelBank to our --input image:
# load the input image and convert it to grayscale
image = cv2.imread(args["image"])
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# loop over the kernels
for (kernelName, kernel) in kernelBank:
# apply the kernel to the grayscale image using both
# our custom `convole` function and OpenCV's `filter2D`
# function
print("[INFO] applying {} kernel".format(kernelName))
convoleOutput = convolve(gray, kernel)
opencvOutput = cv2.filter2D(gray, -1, kernel)
# show the output images
cv2.imshow("original", gray)
cv2.imshow("{} - convole".format(kernelName), convoleOutput)
cv2.imshow("{} - opencv".format(kernelName), opencvOutput)
cv2.waitKey(0)
cv2.destroyAllWindows()
Lines 95 and 96 load our image from disk and convert it to grayscale. Convolution operators can certainly be applied to RGB (or other multi-channel images), but for the sake of simplicity in this blog post, we’ll only apply our filters to grayscale images).
We start looping over our set of kernels in the kernelBank on Line 99 and then apply the current kernel to the gray image on Line 104 by calling our custom convolve method which we defined earlier.
As a sanity check, we also call cv2.filter2D which also applies our kernel to the gray image. The cv2.filter2D function is a much more optimized version of our convolve function. The main reason I included the implementation of convolve in this blog post is to give you a better understanding of how convolutions work under the hood.
Finally, Lines 108-112 display the output images to our screen.
Example Convolutions with OpenCV and Python
Today’s example image comes from a photo I took a few weeks ago at my favorite bar in South Norwalk, CT — Cask Republic. In this image you’ll see a glass of my favorite beer (Smuttynose Findest Kind IPA) along with three 3D-printed Pokemon from the (unfortunately, now closed) Industrial Chimp shop:

To run our script, just issue the following command:
$ python convolutions.py --image 3d_pokemon.png
You’ll then see the results of applying our smallBlur kernel to the input image:

On the left, we have our original image. Then in the center we have the results from the convolve function. And on the right, the results from cv2.filter2D . As the results demonstrate, our output matches cv2.filter2D , indicating that our convolve function is working properly. Furthermore, our original image now appears “blurred” and “smoothed”, thanks to the smoothing kernel.
Next, let’s apply a larger blur:
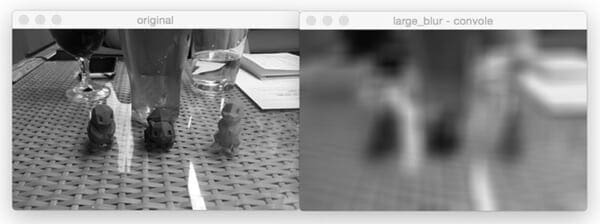
Comparing Figure 7 and Figure 8, notice how as the size of the averaging kernel increases, the amount of blur in the output image increases as well.
We can also sharpen our image:
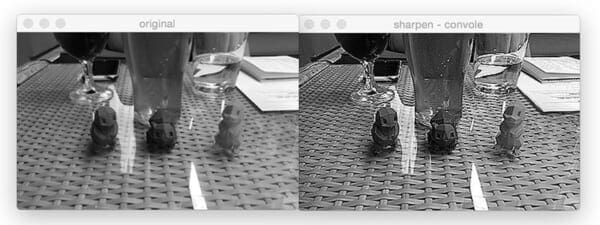
Let’s compute edges using the Laplacian operator:

Find vertical edges with the Sobel operator:

And find horizontal edges using Sobel as well:

The Role of Convolutions in Deep Learning
As you’ve gathered through this blog post, we must manually hand-define each of our kernels for applying various operations such as smoothing, sharpening, and edge detection.
That’s all fine and good, but what if there was a way to learn these filters instead? Is it possible to define a machine learning algorithm that can look at images and eventually learn these types of operators?
In fact, there is — these types of algorithms are a sub-type of Neural Networks called Convolutional Neural Networks (CNNs). By applying convolutional filters, nonlinear activation functions, pooling, and backpropagation, CNNs are able to learn filters that can detect edges and blob-like structures in lower-level layers of the network — and then use the edges and structures as building blocks, eventually detecting higher-level objects (i.e., faces, cats, dogs, cups, etc.) in the deeper layers of the network.
Exactly how do CNNs do this?
I’ll show you — but it will have to wait for another few blog posts until we cover enough basics.
What's next? We recommend PyImageSearch University.
84 total classes • 114+ hours of on-demand code walkthrough videos • Last updated: February 2024
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you'll find:
- ✓ 84 courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 84 Certificates of Completion
- ✓ 114+ hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 536+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Summary
In today’s blog post, we discussed image kernels and convolutions. If we think of an image as a big matrix, then an image kernel is just a tiny matrix that sits on top of the image.
This kernel then slides from left-to-right and top-to-bottom, computing the sum of element-wise multiplications between the input image and the kernel along the way — we call this value the kernel output. The kernel output is then stored in an output image at the same (x, y)-coordinates as the input image (after accounting for any padding to ensure the output image has the same dimensions as the input).
Given our newfound knowledge of convolutions, we defined an OpenCV and Python function to apply a series of kernels to an image. These operators allowed us to blur an image, sharpen it, and detect edges.
Finally, we briefly discussed the roles kernels/convolutions play in deep learning, specifically Convolutional Neural Networks, and how these filters can be learned automatically instead of needing to manually define them first.
In next week’s blog post, I’ll be showing you how to train your first Convolutional Neural Network from scratch using Python — be sure to signup for the PyImageSearch Newsletter using the form below to be notified when the blog post goes live!

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!


Thanks for sharing the concept of `Convolution`. Very clear introductions and simple examples.
No problem, I’m happy I could help introduce the topic Winston! 🙂
Dear Adria
I have a Doubt with this!
This procedure describe the correlation between matrix and not the convolution.
In a convolution we have a minus sign in the middle of the equation, thus we need to turn and swipe the second matrix. Make sense for you?
Hey Juan — thanks for the comment, although I’m not sure I understand your question. Can you please elaborate?
Juan is right. When you’re doing convolution, you’re supposed to flip the kernel both horizontally and vertically in the case od 2D images. Hence the minus sign. It obvisouly doesn’t matter for symmetric kernels like averaging etc., but in general it can lead to nasty bugs for example when trying to accelerate the computation using convolution theorem and FFT.
On the other hand, as far as I’m aware, Caffe framework also only performs correlation in their convolutional layers, while several other libraries do it by the book. So, be aware of these things when trying to convert pre-trained models for instance…
Oh I see — now I understand the question. Thanks for the clarification buchtak.
Hi,
Thanks for this beautifully written post. It very well explains the concept in a simple language. Code example and visuals are real bonus. Keep up the good work.
Thanks!
Thanks, I’m happy I could help!
great job ..
Thank you Vani.
Cool stuff Adrian 😉 A pleasure to read your enthusiasm and excitement 🙂 Keep going!
Thanks Kenny! 🙂
Hi
please tell me which method is the best for detect any object into the large image by using NNs?
Which method is “best” really depends on your application and what you’re actually trying to detect. I would suggest looking into popular object detection frameworks such as YOLO, Faster R-CNNs, and SSDs.
Dear Adrian,
These examples require the skimage library. Is it possible to install that library on the Raspberry Pi 3 model B?
Thanks.
– Ian
Yes, please refer to the scikit-image documentation.
applying a laplacian operation twice, does that correspond to a sqared-laplacian operator?
Why would you take the Laplacian of the Laplacian? Is there a particular reason you need to do that?
Wonderful tutorial. It helped me very much.
Thanks Hygo, I’m glad it was able to help you understand convolutions 🙂
Nice post Adrian,
I wanted to know if there is some method to intuitively de-blur blurred images. Like of course we need to de-convolve with the blur causing kernel but in most practical scenarios we dont know that kernel and resort to brute-force blind de-convolution.
So can we perform blind deconvolution using (say) some ML algorithm?
It really depends on the level of which you are trying to deblur the image. Applying deblurring using a simple kernel is unlikely to give you ideal results. The current state-of-the-art involves applying machine learning to deblur images. Here is a link to a recent NIPS paper so you can learn more about the topic.
Thanks for a great post Adrian,
I encountered a small issue with one of the snippets. I had to convert pad to an int since cv2.copyMakeBorder expects ints as paddings. Thought i`d let you know.
# allocate memory for the output image, taking care to
# “pad” the borders of the input image so the spatial
# size (i.e., width and height) are not reduced
pad = int((kW – 1) / 2)
image = cv2.copyMakeBorder(image, pad, pad, pad, pad,
cv2.BORDER_REPLICATE)
Thanks for sharing Atti! Just to clarify, were you using Python 2.7 or Python 3?
I encountered the same, using Python 3.5.2, opencv 3.1.0. I applied the same fix as Atti.
Thank you for the great blog!
PS:
I used Anaconda 3 to make the whole installation process simpler. Using Anaconda has the added bonus of a more consistent experience between Linux and Win10.
Atti thank you for your message. I also has problem with with this code but I added int (pad = int((kW – 1) / 2)) how you wrote and this code work. Thank you.
Thanks for sharing the post. I’ve subscribed one of your book and really like it.
Thanks for picking up a copy Lugia, I appreciate it!
sir, i encountered this error while running that code… can u help me through this
ubuntu@ubuntu-Inspiron-5559:~/myproject$ python convolutions.py
usage: convolutions.py [-h] -i IMAGE
convolutions.py: error: argument -i/–image is required
You need to supply the
--imagecommand line argument to the script. I would suggest you read up on command line arguments before continuing.Hi Adrian,
wonderful tutorial as all your posts! Thank you.
I need help with an issue I’m running in:
Applying the sharpening filter the call to cv2.filter2D(gray, -1, kernel) run into an exception:
cv2.error: C:\slave\WinInstallerMegaPack\src\opencv\modules\imgproc\src\templmatch.cpp:61: error: (-215) depth == tdepth || tdepth == CV_32F
would be great to get an hint how to solve this.
Many thanks
Gero
Is it only the sharpening kernel? Or all other kernels?
Hi Adrian! Thanks for the amazing post. Although I am a little stuck on the range of ‘for’ loops in convolve function.
Instead of , for e.g. for ‘x’, np.arange(pad, iW + pad), shoudn’t it be just np.arange(pad, iW) since while cutting out the ROI you are considering the extra pad width ( by adding ‘pad’ value to x ) ?
Thank you.
If I understand your question correctly, the
np.arangefunction is non-inclusive on the upper end, hence we add the extra pad value.Thanks for the detailed and clear explanation. I have to define a kernel for a specific template (a part of the image ) and match it with a series of other images. When I do so, The shapes of the kernel and images are not the same. It pops the error message saying “Operands could not be broadcast together ” . Is there a different kind of padding that i should follow?
Thanks in advance 🙂
The shapes of the kernel and image shouldn’t be the same since the kernel essentially slides across the input image. It sounds like you’re not extracting the ROI of the input image correctly before applying the kernel. If the input region is smaller than the kernel size, simply pad the input ROI.
Thanks a lot for demystifying these hard topics.
Thanks for your sharing good information.
I have tested this source code for height 1640, width 1190 bitmap image.
It’s too slow in my VirtualBox Ubuntu 16.04.
Thank you.
We normally don’t process images larger than 600px along its maximum dimension (unless we are applying a specific technique that is geared towards large images). Resize your image and it will run significantly faster.
Hi Adrian,
Great post. BTW, to find scratches from an image (of a metal part) is it a good idea to use convolution?
That really depends on your input images. I’ve never tried to detect scratches on metal but I imagine you might be able to (1) devise a kernel that reveals scratch-like regions or (2) train a network that learns a set of filters that activates under scratch regions.
Hi Adrian!
Thank you for this post! Could you please help me understand how 3D convolutions store color information? Am I able to detect green cats from RGB images if my first convolutional layer uses 3D filters? Or do we use 3D filters to capture information related to shape, edges?
Thank you,
Robert
I assume you are referring to deep learning in which case the convolutions are learned from your input images. If your input images contain green cats then the lower layers of the network will learn color blobs and edge-like regions. Mid-layers of the network combine this information to form contours, outlines, and intersections. The highest layers of the network start to form these semantic concepts such as “cat”, “dog”, etc. CNNs are able to encode color information starting from the input layer.
Thank you for this post! could you please help me how to apply convolution to apply “Directional Weighted Median Filter”. which uses the absolute sum of differences between center pixel and pixels aligned in four main direction, to detect Random valued noise.
I’m also trying to implement the convolution of arbitrary shaped ndarrays in NumPy here:
http://bit.ly/2MhJCex
you may wanna take a look.
Hello sir, ia have a question do you know how the inbuilt convolution function performs this operation ?
I mean the cv2.filter2D or the cuda::createConvolution ?
Thanks a lot sir your post solve all my questions about convolution
I am trying to get convolution output using OpenCV filter2D method and using small matrices however the output given by scipy.signal.convolve2D is correct but cv.filter2d is not correct. Can you please explain. Best
Hi Adrian,
Thank you so much for your detailed explanations. I am using kernels of size 49×49 (from L-M filterbank) on images of size 4800 x 3200. But for some reason I am getting images that are all black. Are there any changes that I have to make in the code to get this working. Kindly let me know what you think could be the problem.
Thanks
I also read the images to read the pixel values. They are almost close to 0. The range of the values is from 15-20.
Check your data type. Are you using a floating point type? If so, convert back to uint8 (which is what OpenCV is expecting).
I am using opencv to read the input image and it is taken as uint8. So, I don’t think that is the problem. The output from your convolve function and the filter2D function from Opencv are different for my images. I am not sure what I am doing wrong.
Do kernels have to be of dtype int?