Today’s blog post is inspired by a question I received from a PyImageSearch reader on Twitter, @makingyouthink.
Paraphrasing the tweets myself and @makingyouthink exchanged, the question was:
Have you ever seen a Python implementation of Measuring colourfulness in natural images (Hasler and Süsstrunk, 2003)?
I would like to use it as an image/produce search engine. By giving each image a “colorfulness” amount, I can sort my images according to their color.
There are many practical uses for image colorfulness, including evaluating compression algorithms, assessing a given camera sensor module’s sensitivity to color, computing the “aesthetic qualities” of an image, or simply creating a bulk image visualization took to show a spectrum of images in a dataset arranged by colorfulness.
Today we are going to learn how to calculate the colorfulness of an image as described in Hasler and Süsstrunk’s 2003 paper, Measuring colorfulness in natural images. We will then implement our colorfulness metric using OpenCV and Python.
After implementing the colorfulness metric, we’ll sort a given dataset according to color and display the results using the image montage tool that we created last week.
To learn about computing image “colorfulness” with OpenCV, just keep reading.
Computing image “colorfulness” with OpenCV and Python
There are three core parts to today’s blog post.
First, we will walk through the colorfulness metric methodology described in in the Hasler and Süsstrunk paper.
We’ll then implement the image colorfulness calculations in Python and OpenCV.
Finally, I’ll demonstrate how we can apply the colorfulness metric to a set of images and sort the images according to how “colorful” they are. We will make use of our handy image montage routine for visualization.
To download the source code + example images to this blog post, be sure to use the “Downloads” section below.
Measuring colorfulness in an image
In their paper, Hasler and Süsstrunk first asked 20 non-expert participants to rate images on a 1-7 scale of colorfulness. This survey was conducted on a set of 84 images. The scale values were:
- Not colorful
- Slightly colorful
- Moderately colorful
- Averagely colorful
- Quite colorful
- Highly colorful
- Extremely colorful
In order to set a baseline, the authors provided the participants with 4 example images and their corresponding colorfulness value from 1-7.
Through a series of experimental calculations, they derived a simple metric that correlated with the results of the viewers.
They found through these experiments that a simple opponent color space representation along with the mean and standard deviations of these values correlates to 95.3% of the survey data.
We now derive their image colorfulness metric:
The above two equations show the opponent color space representation where R is Red, G is Green, and B is Blue. In the first equation, is the difference of the Red channel and the Green channel. In the second equation,
is represents half of the sum of the Red and Green channels minus the Blue channel.
Next, the standard deviation () and mean (
) are computed before calculating the final colorfulness metric,
.
As we’ll find out, this turns out to be an extremely efficient and practical way for computing image colorfulness.
In the next section, we will implement this algorithm with Python and OpenCV code.
Implementing an image colorfulness metric in OpenCV
Now that we have a basic understanding of the colorfulness metric, let’s calculate it with OpenCV and NumPy.
In this section we will:
- Import our necessary Python packages.
- Parse our command line arguments.
- Loop through all images in our dataset and compute the corresponding colorfulness metric.
- Sort the images based on their colorfulness.
- Display the “most colorful” and “least colorful” images in a montage.
To get started open up your favorite text editor or IDE, create a new file named colorfulness.py , and insert the following code:
# import the necessary packages from imutils import build_montages from imutils import paths import numpy as np import argparse import imutils import cv2
Lines 2-7 import our required Python packages.
If you do not have imutils installed on your system (v0.4.3 as of this writing), then make sure you install/upgrade it via pip:
$ pip install --upgrade imutils
Note: If you are using Python virtual environments (as all of my OpenCV install tutorials do), make sure you use the workon command to access your virtual environment first and then install/upgrade imutils .
Next, we will define a new function, image_colorfullness:
def image_colorfulness(image):
# split the image into its respective RGB components
(B, G, R) = cv2.split(image.astype("float"))
# compute rg = R - G
rg = np.absolute(R - G)
# compute yb = 0.5 * (R + G) - B
yb = np.absolute(0.5 * (R + G) - B)
# compute the mean and standard deviation of both `rg` and `yb`
(rbMean, rbStd) = (np.mean(rg), np.std(rg))
(ybMean, ybStd) = (np.mean(yb), np.std(yb))
# combine the mean and standard deviations
stdRoot = np.sqrt((rbStd ** 2) + (ybStd ** 2))
meanRoot = np.sqrt((rbMean ** 2) + (ybMean ** 2))
# derive the "colorfulness" metric and return it
return stdRoot + (0.3 * meanRoot)
Line 9 defines the image_colorfulness function, which takes an image as the only argument and returns the colorfulness metric as described in the section above.
Note: Line 11, Line 14, and Line 17 make use of color spaces which are beyond the scope of this blog post. If you are interested in learning more about color spaces, be sure to refer to Practical Python and OpenCV and the PyImageSearch Gurus course.
To break the image into it’s Red, Green, and Blue (RGB) channels we make a call to cv2.split on Line 11. The function returns a tuple in BGR order as this is how images are represented in OpenCV.
Next we use a very simple opponent color space.
As in the referenced paper, we compute the Red-Green opponent, rg, on Line 14. This is a simple difference of the Red channel minus the Blue channel.
Similarly, we compute the Yellow-Blue opponent on Line 17. In this calculation, we take half of the Red+Green channel sum and then subtract the Blue channel. This produces our desired opponent, yb.
From there, on Lines 20 and 21 we compute the mean and standard deviation of both rg and yb, and store them in respective tuples.
Next, we combine the rbStd (Red-Blue standard deviation) with the ybStd (Yellow-Blue standard deviation) on Line 24. We add the square of each and then take the square root, storing it as stdRoot.
Similarly, we combine the rbMean with the ybMean by squaring each, adding them, and taking the square root on Line 25. We store this value as meanRoot.
The last step of computing image colorfulness is to add stdRoot and 1/3 meanRoot followed by returning the value to the calling function.
Now that our image image_colorfulness metric is defined, we can parse our command line arguments:
# construct the argument parse and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-i", "--images", required=True,
help="path to input directory of images")
args = vars(ap.parse_args())
We only need one command line argument here, --images , which is the path to a directory of images residing on your machine.
Now let’s loop through each image in the dataset and compute the corresponding colorfulness metric:
# initialize the results list
print("[INFO] computing colorfulness metric for dataset...")
results = []
# loop over the image paths
for imagePath in paths.list_images(args["images"]):
# load the image, resize it (to speed up computation), and
# compute the colorfulness metric for the image
image = cv2.imread(imagePath)
image = imutils.resize(image, width=250)
C = image_colorfulness(image)
# display the colorfulness score on the image
cv2.putText(image, "{:.2f}".format(C), (40, 40),
cv2.FONT_HERSHEY_SIMPLEX, 1.4, (0, 255, 0), 3)
# add the image and colorfulness metric to the results list
results.append((image, C))
Line 38 initializes a list, results , which will hold a 2-tuple containing the image path and the corresponding colorfulness of the image.
We begin our loop through our images in our dataset specified by our command line argument, --images on Line 41.
In the loop, we first load the image on Line 44, then we resize the image to a width=250 pixels on Line 45, maintaining the aspect ratio.
Our image_colorfulness function call is made on Line 46 where we provide the only argument, image, storing the corresponding colorfulness metric in C.
On Lines 49 and 50, we draw the colorfulness metric on the image using cv2.putText. To read more about the parameters to this function, see the OpenCV Documentation (2.4, 3.0).
On the last line of the for loop, we append the tuple, (imagePath, C) to the results list (Line 53).
Note: Typically, you would not want to store each image in memory for a large dataset. We do this here for convenience. In practice you would load the image, compute the colorfulness metric, and then maintain a list of the image ID/filename and corresponding colorfulness metric. This is a much more efficient approach; however, for the sake of this example we are going to store the images in memory so we can easily build our montage of “most colorful” and “least colorful” images later in the tutorial.
At this point, we have answered our PyImageSearch reader’s question. The colorfulness metric has been calculated for all images.
If you’re using this for an image search engine as @makingyouthinkcom is, you probably want to display your results.
And that is exactly what we will do next, where we will:
- Sort the images according to their corresponding colorfulness metric.
- Determine the 25 most colorful and 25 least colorful images.
- Display our results in a montage.
Let’s go ahead and tackle these three tasks now:
# sort the results with more colorful images at the front of the
# list, then build the lists of the *most colorful* and *least
# colorful* images
print("[INFO] displaying results...")
results = sorted(results, key=lambda x: x[1], reverse=True)
mostColor = [r[0] for r in results[:25]]
leastColor = [r[0] for r in results[-25:]][::-1]
On Line 59 we sort the results in reverse order (according to their colorfulness metric) making use of Python Lambda Expressions.
Then on Line 60, we store the 25 most colorful images into a list, mostColor .
Similarly, on Line 61, we load the least colorful images which are the last 25 images in our results list. We reverse this list so that the images are displayed in ascending order. We store these images as leastColor .
Now, we can visualize the mostColor and leastColor images using the build_montages function we learned about last week.
# construct the montages for the two sets of images mostColorMontage = build_montages(mostColor, (128, 128), (5, 5)) leastColorMontage = build_montages(leastColor, (128, 128), (5, 5))
A most-colorful and least-colorful montage are each built on Lines 64 and 65. Here we indicate that all images in the montage will be resized to 128 x 128 and there will be 5 columns by 5 rows of images.
Now that we have assembled the montages, we will display each on the screen.
# display the images
cv2.imshow("Most Colorful", mostColorMontage[0])
cv2.imshow("Least Colorful", leastColorMontage[0])
cv2.waitKey(0)
On Lines 68 and 69 we display each montage in a separate window.
The cv2.waitKey call on Line 70 pauses execution of our script until we select a currently active window. When a key is pressed, the windows close and the script exits.
Image colorfulness results
Now let’s put this script to work and see the results. Today we will use a sample (1,000 images) of the popular UKBench dataset, a collection of images containing everyday objects.
Our goal is to sort the images by most colorful and least colorful.
To run the script, fire up a terminal and execute the following command:
$ python colorfulness.py --images ukbench_sample
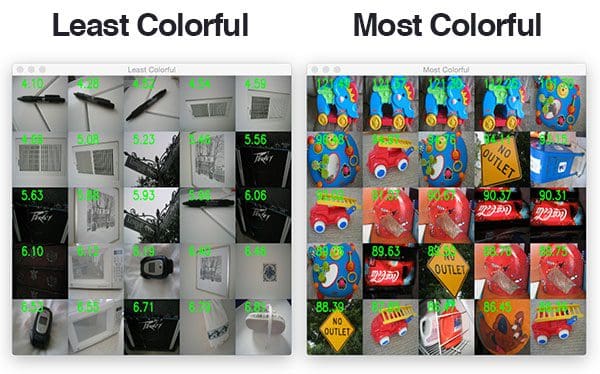
Notice how our image colorfulness metric has done a good job separating non-colorful images (left) that are essentially black and white from “colorful” images that are vibrant (right).
What's next? We recommend PyImageSearch University.
84 total classes • 114+ hours of on-demand code walkthrough videos • Last updated: February 2024
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you'll find:
- ✓ 84 courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 84 Certificates of Completion
- ✓ 114+ hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 536+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Summary
In today’s blog post we learned how to compute the “colorfulness” of an image using the approach detailed by Hasler and Süsstrunk’s in their 2003 paper, Measuring colorfulness in nature images.
Their method is based on the mean and standard deviation of pixel intensities values in an opponent color space. This metric was derived by examining correlations between experimental metrics and the colorfulness assigned to images by participants in their study.
We then implemented the image colorfulness metric and applied it to the UKBench dataset. As our results demonstrated, the Hasler and Süsstrunk method is a quick and easy way to quantify the colorfulness contents of an image.
Have fun using this method to experiment with the image colorfulness in your own datasets!
And before you go, be sure to enter your email address in the form below to be notified when new tutorials are published here on the PyImageSearch blog.

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!

