I have issues — I can’t stop thinking about object detection.
You see, last night I was watching The Walking Dead and instead of enjoying the zombie brutality, the forced cannibalism, or the enthralling storyline, all I wanted to do was build an object detection system to recognize zombies.
Would it be very useful? Probably not.
I mean, it’s quite obvious if a zombie is coming after you. The stench alone should be a dead (hey, look at that pun) giveaway, let alone the gnashing of teeth and outstretched arms. And we might as well throw in guttural “brainnnnsss” moans as well.
Like I said, it would be pretty obvious if a zombie was after you — you certainly wouldn’t need a computer vision system to tell you that. But this is just an example of the type of stuff that runs through my head on a day-to-day basis.
To give you some context, two weeks ago I posted about using Histogram of Oriented Gradients and a Linear Support Vector Machine to build an object detection system. Sick of using the OpenCV Haar cascades and obtaining poor performance, and not to mention, extremely long training times, I took it upon myself to write my own Python object detection framework.
So far, it’s gone extremely well and it’s been a lot of fun to implement.
But there’s an unescapable issue you must handle when building an object detection system — overlapping bounding boxes. It’s going to happen, there’s no way around it. In fact, it’s actually a good sign that your object detector is firing properly so I wouldn’t even call it an “issue” exactly.
To handle the removal overlapping bounding boxes (that refer to the same object) we can either use non-maximum suppression on the Mean-Shift algorithm. While Dalal and Triggs prefer Mean-Shift, I find Mean-Shift to give sub-par results.
After receiving advice from my friend (and expert on object detection), Dr. Tomasz Malisiewicz, I decided to port his non-maximum suppression MATLAB implementations over to Python.
Last week I showed you how to implement the Felzenszwalb et al. method. And this week I am going to show you the Malisiewicz et al. method which is over 100x faster.
Note: I intended on publishing this blog post way back in November, but due to some poor planning on my part, it’s taken awhile for me to get this post out the door. Anyway, it’s online now!
So where does the speedup come from? And how do we obtain such faster suppression times?
Read on to find out.
OpenCV and Python versions:
This example will run on Python 2.7/Python 3.4+ and OpenCV 2.4.X/OpenCV 3.0+.
(Faster) Non-Maximum Suppression in Python
Before we get started, if you haven’t read last week’s post on non-maximum suppression, I would definitely start there.
Otherwise, open up a new file in your favorite editor, name it nms.py , and let’s get started on creating a faster non-maximum suppression implementation:
# import the necessary packages
import numpy as np
# Malisiewicz et al.
def non_max_suppression_fast(boxes, overlapThresh):
# if there are no boxes, return an empty list
if len(boxes) == 0:
return []
# if the bounding boxes integers, convert them to floats --
# this is important since we'll be doing a bunch of divisions
if boxes.dtype.kind == "i":
boxes = boxes.astype("float")
# initialize the list of picked indexes
pick = []
# grab the coordinates of the bounding boxes
x1 = boxes[:,0]
y1 = boxes[:,1]
x2 = boxes[:,2]
y2 = boxes[:,3]
# compute the area of the bounding boxes and sort the bounding
# boxes by the bottom-right y-coordinate of the bounding box
area = (x2 - x1 + 1) * (y2 - y1 + 1)
idxs = np.argsort(y2)
# keep looping while some indexes still remain in the indexes
# list
while len(idxs) > 0:
# grab the last index in the indexes list and add the
# index value to the list of picked indexes
last = len(idxs) - 1
i = idxs[last]
pick.append(i)
# find the largest (x, y) coordinates for the start of
# the bounding box and the smallest (x, y) coordinates
# for the end of the bounding box
xx1 = np.maximum(x1[i], x1[idxs[:last]])
yy1 = np.maximum(y1[i], y1[idxs[:last]])
xx2 = np.minimum(x2[i], x2[idxs[:last]])
yy2 = np.minimum(y2[i], y2[idxs[:last]])
# compute the width and height of the bounding box
w = np.maximum(0, xx2 - xx1 + 1)
h = np.maximum(0, yy2 - yy1 + 1)
# compute the ratio of overlap
overlap = (w * h) / area[idxs[:last]]
# delete all indexes from the index list that have
idxs = np.delete(idxs, np.concatenate(([last],
np.where(overlap > overlapThresh)[0])))
# return only the bounding boxes that were picked using the
# integer data type
return boxes[pick].astype("int")
Take a second to really examine this code and compare it to the Felzenszwalb et al. implementation of last week.
The code looks almost identical, right?
So you’re probably asking yourself “Where does this 100x speed-up come from?”
And the answer is the removal of an inner for loop.
The implementation from last week required an extra inner for loop to compute the size of bounding regions and compute the ratio of overlapped area.
Instead, Dr. Malisiewicz replaced this inner for loop with vectorized code — and this is how we are able to achieve substantially faster speeds when applying non-maximum suppression.
Instead of repeating myself and going line-by-line through the code like I did last week, let’s just examine the important parts.
Lines 6-22 of our faster non-maximum suppression function are essentially the same as they are from last week. We start by grabbing the (x, y) coordinates of the bounding boxes, computing their area, and sorting the indexes into the boxes list according to their bottom-right y-coordinate of each box.
Lines 31-55 contain our speed-up, where Lines 41-55 are especially important.
Instead of using an inner for loop to loop over each of the individual boxes, we instead vectorize the code using the np.maximum and np.minimum functions — this allows us to find the maximum and minimum values across the axis rather than just individual scalars.
Note: You have to use the np.maximum and np.minimum functions here — they allow you to mix scalars and vectors. The np.max and np.min functions do not, and if you use them, you will find yourself with some pretty fierce bugs to find and fix. It took me quite awhile to debug this problem when I was porting the algorithm from MATLAB to Python.
Lines 47 and 48 are also vectorized — here we compute the width and height of each of the rectangles to check. Similarly, computing the overlap ratio on Line 51 is also vectorized. From there, we just delete all entries from our idx list that are greater than our supplied overlap threshold. Typical values for the overlap threshold normally fall in the range 0.3-0.5.
The Malisiewicz et al. method is essentially identical to the Felzenszwalb et al. method, but by using vectorized code we are able to reach a reported 100x speed-up in non-maximum suppression!
Faster Non-Maximum Suppression in Action
Let’s go ahead and explore a few examples. We’ll start with the creepy little girl zombie that we saw at the top of this image:

It’s actually really funny how well our face detector trained on real, healthy human faces generalizes to zombie faces as well. Granted, they are still “human” faces, but with all the blood and disfigurement, I wouldn’t be surprised to see some strange results.

Speaking of strange results, it looks like our face detector detected the mouth/teeth region of the zombie on the right. Perhaps if I had explicitly trained the HOG + Linear SVM face detector on zombie images the results would be better.
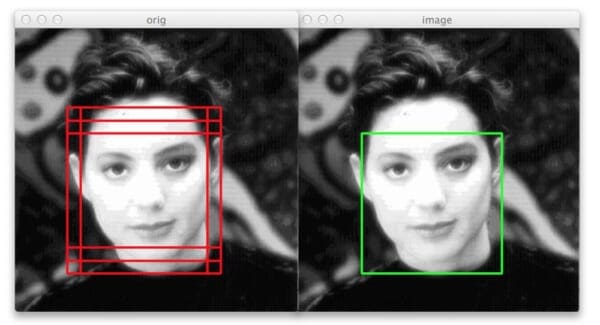
In this last example we can again see that our non-maximum suppression algorithm is working correctly — even though six original bounding boxes were detected by the HOG + Linear SVM detector, applying non-maximum suppression has correctly suppressed five of the boxes, leaving us with the final detection.
What's next? We recommend PyImageSearch University.
84 total classes • 114+ hours of on-demand code walkthrough videos • Last updated: February 2024
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you'll find:
- ✓ 84 courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 84 Certificates of Completion
- ✓ 114+ hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 536+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Summary
In this blog post we reviewed the Malisiewicz et al. method for non-maximum suppression.
This method is nearly identical to the Felzenszwalb et al. method, but by removing an inner for loop and using vectorized code we are able to obtain substantial speed-ups.
And if you have a second, be sure to thank Dr. Tomasz Malisiewicz!

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!

