Many strategies used in machine learning are explicitly designed to reduce the test error, possibly at the expense of increased training error. These strategies are collectively known as regularization.
—Goodfellow, Bengio, and Courville (2016)
In previous lessons, we discussed two important loss functions: Multi-class SVM loss and cross-entropy loss. We then discussed gradient descent and how a network can actually learn by updating the weight parameters of a model. While our loss function allows us to determine how well (or poorly) our set of parameters are performing on a given classification task, the loss function itself does not take into account how the weight matrix “looks.”

What do I mean by “looks”? Well, keep in mind that we are working in a real-valued space, thus there are an infinite set of parameters that will obtain reasonable classification accuracy on our dataset (for some definition of “reasonable”).
How do we go about choosing a set of parameters that help ensure our model generalizes well? Or, at the very least, lessen the effects of overfitting. The answer is regularization. Second only to your learning rate, regularization is the most important parameter of your model that you can tune.
There are various types of regularization techniques, such as L1 regularization, L2 regularization (commonly called “weight decay”), and Elastic Net, that are used by updating the loss function itself, adding an additional parameter to constrain the capacity of the model.
We also have types of regularization that can be explicitly added to the network architecture — dropout is the quintessential example of such regularization. We then have implicit forms of regularization that are applied during the training process. Examples of implicit regularization include data augmentation and early stopping.
What Is Regularization and Why Do We Need It?
Regularization helps us control our model capacity, ensuring that our models are better at making (correct) classifications on data points that they were not trained on, which we call the ability to generalize. If we don’t apply regularization, our classifiers can easily become too complex and overfit to our training data, in which case we lose the ability to generalize to our testing data (and data points outside the testing set as well, such as new images in the wild).
However, too much regularization can be a bad thing. We can run the risk of underfitting, in which case our model performs poorly on the training data and is not able to model the relationship between the input data and output class labels (because we limited model capacity too much). For example, consider the following plot of points, along with various functions that fit to these points (Figure 1).
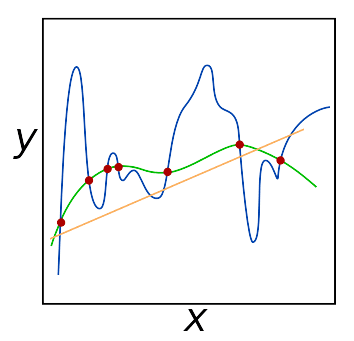
The orange line is an example of underfitting — we are not capturing the relationship between the points. On the other hand, the blue line is an example of overfitting — we have too many parameters in our model, and while it hits all points in the dataset, it also wildly varies between the points. It is not a smooth, simple fit that we would prefer. We then have the green function which also hits all points in our dataset, but does so in a much more predictable, simple manner.
The goal of regularization is to obtain these types of “green functions” that fit our training data nicely, but avoid overfitting to our training data (blue) or failing to model the underlying relationship (orange). Regularization is a critical aspect of machine learning and we use regularization to control model generalization. To understand regularization and the impact it has on our loss function and weight update rule, let’s proceed to the next lesson.
Updating Our Loss and Weight Update to Include Regularization
Let’s start with our cross-entropy loss function:
(1)
The loss over the entire training set can be written as:
(2)
Now, let’s say that we have obtained a weight matrix W such that every data point in our training set is classified correctly, which means that our loss L = 0 for all Li.
Awesome, we’re getting 100% accuracy — but let me ask you a question about this weight matrix — is it unique? Or, in other words, are there better choices of W that will improve our model’s ability to generalize and reduce overfitting?
If there is such a W, how do we know? And how can we incorporate this type of penalty into our loss function? The answer is to define a regularization penalty, a function that operates on our weight matrix. The regularization penalty is commonly written as a function, R(W). Equation (3) shows the most common regularization penalty, L2 regularization (also called weight decay):
(3)
What is the function doing exactly? In terms of Python code, it’s simply taking the sum of squares over an array:
penalty = 0 for i in np.arange(0, W.shape[0]): for j in np.arange(0, W.shape[1]): penalty += (W[i][j] ** 2)
What we are doing here is looping over all entries in the matrix and taking the sum of squares. The sum of squares in the L2 regularization penalty discourages large weights in our matrix W, preferring smaller ones. Why might we want to discourage large weight values? In short, by penalizing large weights, we can improve the ability to generalize, and thereby reduce overfitting.
Think of it this way — the larger a weight value is, the more influence it has on the output prediction. Dimensions with larger weight values can almost singlehandedly control the output prediction of the classifier (provided the weight value is large enough, of course) which will almost certainly lead to overfitting.
To mitigate the effect various dimensions have on our output classifications, we apply regularization, thereby seeking W values that take into account all of the dimensions rather than the few with large values. In practice you may find that regularization hurts your training accuracy slightly, but actually increases your testing accuracy.
Again, our loss function has the same basic form, only now we add in regularization:
(4)
The first term we have seen before — it is the average loss over all samples in our training set.
The second term is new — this is our regularization penalty. The λ variable is a hyperparameter that controls the amount or strength of the regularization we are applying. In practice, both the learning rate α and the regularization term λ are the hyperparameters that you’ll spend the most time tuning.
Expanding cross-entropy loss to include L2 regularization yields the following equation:
(5)
We can also expand Multi-class SVM loss as well:
(6)
Now, let’s take a look at our standard weight update rule:
(7) W = W −α∇W f(W)
This method updates our weights based on the gradient multiplied by a learning rate α. Taking into account regularization, the weight update rule becomes:
(8) W = W −α∇W f(W)−λR(W)
Here, we are adding a negative linear term to our gradients (i.e., gradient descent), penalizing large weights, with the end goal of making it easier for our model to generalize.
Types of Regularization Techniques
In general, you’ll see three common types of regularization that are applied directly to the loss function. The first, we reviewed earlier, L2 regularization (aka “weight decay”):
(9)
We also have L1 regularization which takes the absolute value rather than the square:
(10)
Elastic Net regularization seeks to combine both L1 and L2 regularization:
(11)
Other types of regularization methods exist such as directly modifying the architecture of a network along with how the network is actually trained — we will review these methods in later lessons.
In terms of which regularization method you should be using (including none at all), you should treat this choice as a hyperparameter you need to optimize over and perform experiments to determine if regularization should be applied, and if so which method of regularization, and what the proper value of λ is. For more details on regularization, refer to Chapter 7 of Goodfellow et al. (2016), the “Regularization” section from the DeepLearning.net tutorial, and the notes from Karpathy’s cs231n Neural Networks II lecture.
Regularization Applied to Image Classification
To demonstrate regularization in action, let’s write some Python code to apply it to our “Animals” dataset. Open a new file, name it regularization.py, and insert the following code:
# import the necessary packages from sklearn.linear_model import SGDClassifier from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import train_test_split from pyimagesearch.preprocessing import SimplePreprocessor from pyimagesearch.datasets import SimpleDatasetLoader from imutils import paths import argparse
Lines 2-8 import our required Python packages. We’ve seen all of these imports before, except the scikit-learn SGDClassifier. As the name of this class suggests, this implementation encapsulates all the concepts we have reviewed in our lessons, including:
- Loss functions
- Number of epochs
- Learning rate
- Regularization terms
Thus making it the perfect example to demonstrate all these concepts in action.
Next, we can parse our command line arguments and grab the list of images from disk:
# construct the argument parse and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-d", "--dataset", required=True,
help="path to input dataset")
args = vars(ap.parse_args())
# grab the list of image paths
print("[INFO] loading images...")
imagePaths = list(paths.list_images(args["dataset"]))
Given the image paths, we’ll resize them to 32×32 pixels, load them from disk into memory, and then flatten them into a 3,072-dim array:
# initialize the image preprocessor, load the dataset from disk, # and reshape the data matrix sp = SimplePreprocessor(32, 32) sdl = SimpleDatasetLoader(preprocessors=[sp]) (data, labels) = sdl.load(imagePaths, verbose=500) data = data.reshape((data.shape[0], 3072))
We’ll also encode the labels as integers and perform a training testing split, using 75% of the data for training and the remaining 25% for testing:
# encode the labels as integers le = LabelEncoder() labels = le.fit_transform(labels) # partition the data into training and testing splits using 75% of # the data for training and the remaining 25% for testing (trainX, testX, trainY, testY) = train_test_split(data, labels, test_size=0.25, random_state=42)
Let’s apply a few different types of regularization when training our SGDClassifier:
# loop over our set of regularizers
for r in (None, "l1", "l2"):
# train a SGD classifier using a softmax loss function and the
# specified regularization function for 10 epochs
print("[INFO] training model with '{}' penalty".format(r))
model = SGDClassifier(loss="log", penalty=r, max_iter=10,
learning_rate="constant", tol=1e-3, eta0=0.01, random_state=12)
model.fit(trainX, trainY)
# evaluate the classifier
acc = model.score(testX, testY)
print("[INFO] {} penalty accuracy: {:.2f}%".format(r,
acc * 100))
Line 37 loops over our regularizers, including no regularization. We then initialize and train the SGDClassifier on Lines 41-43.
We’ll be using cross-entropy loss, with regularization penalty of r and a default λ of 0.0001. We’ll use SGD to train the model for 10 epochs with a learning rate of α = 0.01. We then evaluate the classifier and display the accuracy results to our screen on Lines 46-48.
To see our SGD model trained with various regularization types, just execute the following command:
$ python regularization.py --dataset dataset/animals [INFO] loading images... ... [INFO] training model with 'None' penalty [INFO] 'None' penalty accuracy: 50.13% [INFO] training model with 'l1' penalty [INFO] 'l1' penalty accuracy: 52.67% [INFO] training model with 'l2' penalty [INFO] 'l2' penalty accuracy: 57.20%
We can see with no regularization we obtain an accuracy of 50.13%. Using L1 regularization our accuracy increases to 52.67%. L2 regularization obtains the highest accuracy of 57.20%.
Remark: Using different random_state values for train_test_split will yield different results. The dataset here is too small and the classifier too simplistic to see the full impact of regularization, so consider this a “worked example.” As we continue to work through this book you’ll see more advanced uses of regularization that will have dramatic impacts on your accuracy.
Realistically, this example is too small to show all the advantages of applying regularization — for that, we’ll have to wait until we start training Convolutional Neural Networks. However, in the meantime simply appreciate that regularization can provide a boost in our testing accuracy and reduce overfitting, provided we can tune the hyperparameters right.
What's next? We recommend PyImageSearch University.
84 total classes • 114+ hours of on-demand code walkthrough videos • Last updated: February 2024
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you'll find:
- ✓ 84 courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 84 Certificates of Completion
- ✓ 114+ hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 536+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Summary
In these lessons, we popped the hood on deep learning and took a deep dive into the engine that powers modern day neural networks — gradient descent. We investigated two types of gradient descent:
- The standard vanilla flavor.
- The stochastic version that is more commonly used.
Vanilla gradient descent performs only one weight update per epoch, making it very slow (if not impossible) to converge on large datasets. The stochastic version instead applies multiple weight updates per epoch by computing the gradient on small mini-batches. By using SGD we can dramatically reduce the time it takes to train a model while also enjoying lower loss and higher accuracy. Typical batch sizes include 32, 64, 128, and 256.
Gradient descent algorithms are controlled via a learning rate: this is by far the most important parameter to tune correctly when training your own models.
If your learning rate is too large, you’ll simply bounce around the loss landscape and not actually “learn” any patterns from your data. On the other hand, if your learning rate is too small, it will take a prohibitive number of iterations to reach even a reasonable loss. To get it just right, you’ll want to spend the majority of your time tuning the learning rate.
We then discussed regularization, which is defined as “any method that increases testing accuracy perhaps at the expense of training accuracy.” Regularization encompasses a broad range of techniques. We specifically focused on regularization methods that are applied to our loss functions and weight update rules, including L1 regularization, L2 regularization, and Elastic Net.
In terms of deep learning and neural networks, you’ll commonly see L2 regularization used for image classification — the trick is tuning the λ parameter to include just the right amount of regularization.
At this point, we have a sound foundation of machine learning, but we have yet to investigate neural networks or train a custom neural network from scratch. That will all change in a future lesson, where we discuss neural networks, the backpropagation algorithm, and how to train your own neural networks on custom datasets.

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!
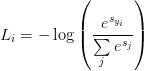
![L = \displaystyle\frac{1}{N} \sum\limits^{N}_{i=1}\left [-\log\left(\displaystyle\frac{e^{s_{y_{i}}}}{\sum\limits_{j} e^{s_{j}}}\right)\right] +\lambda \sum\limits_{i} \sum\limits_{j} W_{i, j}^{2} L = \displaystyle\frac{1}{N} \sum\limits^{N}_{i=1}\left [-\log\left(\displaystyle\frac{e^{s_{y_{i}}}}{\sum\limits_{j} e^{s_{j}}}\right)\right] +\lambda \sum\limits_{i} \sum\limits_{j} W_{i, j}^{2}](https://b2633864.smushcdn.com/2633864/wp-content/latex/5bf/5bfe1feb681423e45ff2b4e1b8775b00-ffffff-000000-0.png?size=327x71&lossy=2&strip=1&webp=1)
![L = \displaystyle\frac{1}{N} \sum\limits^{N}_{i=1} \sum\limits_{j \neq y_{i}} \left[\max\left(0, s_{j} - s_{y_{i}} + 1\right)\right] + \lambda \sum\limits_{i} \sum\limits_{j} W_{i, j}^{2} L = \displaystyle\frac{1}{N} \sum\limits^{N}_{i=1} \sum\limits_{j \neq y_{i}} \left[\max\left(0, s_{j} - s_{y_{i}} + 1\right)\right] + \lambda \sum\limits_{i} \sum\limits_{j} W_{i, j}^{2}](https://b2633864.smushcdn.com/2633864/wp-content/latex/70d/70df09533556d88d6421d1683adf40ae-ffffff-000000-0.png?size=372x51&lossy=2&strip=1&webp=1)

