In the previous section, we discussed gradient descent, a first-order optimization algorithm that can be used to learn a set of classifier weights for parameterized learning. However, this “vanilla” implementation of gradient descent can be prohibitively slow to run on large datasets — in fact, it can even be considered computationally wasteful.
Instead, we should apply Stochastic Gradient Descent (SGD), a simple modification to the standard gradient descent algorithm that computes the gradient and updates the weight matrix W on small batches of training data, rather than the entire training set. While this modification leads to “more noisy” updates, it also allows us to take more steps along the gradient (one step per each batch versus one step per epoch), ultimately leading to faster convergence and no negative effects to loss and classification accuracy.
SGD is arguably the most important algorithm when it comes to training deep neural networks. Even though the original incarnation of SGD was introduced over 57 years ago (Stanford Electronics Laboratories et al., 1960), it is still the engine that enables us to train large networks to learn patterns from data points. Above all other algorithms covered in this book, take the time to understand SGD.
Mini-batch SGD
Reviewing the vanilla gradient descent algorithm, it should be (somewhat) obvious that the method will run very slowly on large datasets. The reason for this slowness is because each iteration of gradient descent requires us to compute a prediction for each training point in our training data before we are allowed to update our weight matrix. For image datasets such as ImageNet where we have over 1.2 million training images, this computation can take a long time.
It also turns out that computing predictions for every training point before taking a step along our weight matrix is computationally wasteful and does little to help our model coverage.
Instead, what we should do is batch our updates. We can update the pseudocode to transform vanilla gradient descent to become SGD by adding an extra function call:
while True: batch = next_training_batch(data, 256) Wgradient = evaluate_gradient(loss, batch, W) W += -alpha * Wgradient
The only difference between vanilla gradient descent and SGD is the addition of the next_training_batch function. Instead of computing our gradient over the entire data set, we instead sample our data, yielding a batch. We evaluate the gradient on the batch, and update our weight matrix W. From an implementation perspective, we also try to randomize our training samples before applying SGD since the algorithm is sensitive to batches.
After looking at the pseudocode for SGD, you’ll immediately notice an introduction of a new parameter: the batch size. In a “purist” implementation of SGD, your mini-batch size would be 1, implying that we would randomly sample one data point from the training set, compute the gradient, and update our parameters. However, we often use mini-batches that are > 1. Typical batch sizes include 32, 64, 128, and 256.
So, why bother using batch sizes > 1? To start, batch sizes > 1 help reduce variance in the parameter update (http://pyimg.co/pd5w0), leading to a more stable convergence. Secondly, powers of two are often desirable for batch sizes as they allow internal linear algebra optimization libraries to be more efficient.
In general, the mini-batch size is not a hyperparameter you should worry too much about (http://cs231n.stanford.edu). If you’re using a GPU to train your neural network, you determine how many training examples will fit into your GPU and then use the nearest power of two as the batch size such that the batch will fit on the GPU. For CPU training, you typically use one of the batch sizes listed above to ensure you reap the benefits of linear algebra optimization libraries.
Implementing Mini-batch SGD
Let’s go ahead and implement SGD and see how it differs from standard vanilla gradient descent. Open a new file, name it sgd.py, and insert the following code:
# import the necessary packages from sklearn.model_selection import train_test_split from sklearn.metrics import classification_report from sklearn.datasets import make_blobs import matplotlib.pyplot as plt import numpy as np import argparse def sigmoid_activation(x): # compute the sigmoid activation value for a given input return 1.0 / (1 + np.exp(-x)) def sigmoid_deriv(x): # compute the derivative of the sigmoid function ASSUMING # that the input "x" has already been passed through the sigmoid # activation function return x * (1 - x)
Lines 2-7 import our required Python packages, exactly the same as the gradient_descent.py example earlier in this chapter. Lines 9-17 define our sigmoid_activation and sigmoid_deriv functions, both of which are identical to the previous version of gradient descent.
In fact, the predict method doesn’t change either:
def predict(X, W): # take the dot product between our features and weight matrix preds = sigmoid_activation(X.dot(W)) # apply a step function to threshold the outputs to binary # class labels preds[preds <= 0.5] = 0 preds[preds > 0] = 1 # return the predictions return preds
However, what does change is the addition of the next_batch function:
def next_batch(X, y, batchSize): # loop over our dataset "X" in mini-batches, yielding a tuple of # the current batched data and labels for i in np.arange(0, X.shape[0], batchSize): yield (X[i:i + batchSize], y[i:i + batchSize])
The next_batch method requires three parameters:
X: Our training dataset of feature vectors/raw image pixel intensities.y: The class labels associated with each of the training data points.batchSize: The size of each mini-batch that will be returned.
Lines 34 and 35 then loop over the training examples, yielding subsets of both X and y as mini-batches.
Next, we can parse our command line arguments:
# construct the argument parse and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-e", "--epochs", type=float, default=100,
help="# of epochs")
ap.add_argument("-a", "--alpha", type=float, default=0.01,
help="learning rate")
ap.add_argument("-b", "--batch-size", type=int, default=32,
help="size of SGD mini-batches")
args = vars(ap.parse_args())
We have already reviewed both the --epochs (number of epochs) and --alpha (learning rate) switch from the vanilla gradient descent example — but also notice we are introducing a third switch: --batch-size, which as the name indicates is the size of each of our mini-batches. We’ll default this value to be 32 data points per mini-batch.
Our next code block handles generating our 2-class classification problem with 1,000 data points, adding the bias column, and then performing the training and testing split:
# generate a 2-class classification problem with 1,000 data points, # where each data point is a 2D feature vector (X, y) = make_blobs(n_samples=1000, n_features=2, centers=2, cluster_std=1.5, random_state=1) y = y.reshape((y.shape[0], 1)) # insert a column of 1's as the last entry in the feature # matrix -- this little trick allows us to treat the bias # as a trainable parameter within the weight matrix X = np.c_[X, np.ones((X.shape[0]))] # partition the data into training and testing splits using 50% of # the data for training and the remaining 50% for testing (trainX, testX, trainY, testY) = train_test_split(X, y, test_size=0.5, random_state=42)
We’ll then initialize our weight matrix and losses just like in the previous example:
# initialize our weight matrix and list of losses
print("[INFO] training...")
W = np.random.randn(X.shape[1], 1)
losses = []
The real change comes next where we loop over the desired number of epochs, sampling mini-batches along the way:
# loop over the desired number of epochs for epoch in np.arange(0, args["epochs"]): # initialize the total loss for the epoch epochLoss = [] # loop over our data in batches for (batchX, batchY) in next_batch(trainX, trainY, args["batch_size"]): # take the dot product between our current batch of features # and the weight matrix, then pass this value through our # activation function preds = sigmoid_activation(batchX.dot(W)) # now that we have our predictions, we need to determine the # "error", which is the difference between our predictions # and the true values error = preds - batchY epochLoss.append(np.sum(error ** 2))
On Line 69, we start looping over the supplied number of --epochs. We then loop over our training data in batches on Line 74. For each batch, we compute the dot product between the batch and W, then pass the result through the sigmoid activation function to obtain our predictions. We compute the error for the batch on Line 83 and use this value to update our least squares epochLoss on Line 84.
Now that we have the error, we can compute the gradient descent update, identical to computing the gradient from vanilla gradient descent, only this time we are performing the update on batches rather than the entire training set:
# the gradient descent update is the dot product between our # (1) current batch and (2) the error of the sigmoid # derivative of our predictions d = error * sigmoid_deriv(preds) gradient = batchX.T.dot(d) # in the update stage, all we need to do is "nudge" the # weight matrix in the negative direction of the gradient # (hence the term "gradient descent" by taking a small step # towards a set of "more optimal" parameters W += -args["alpha"] * gradient
Line 96 handles updating our weight matrix based on the gradient, scaled by our learning rate --alpha. Notice how the weight update stage takes place inside the batch loop — this implies there are multiple weight updates per epoch.
We can then update our loss history by taking the average across all batches in the epoch and then displaying an update to our terminal if necessary:
# update our loss history by taking the average loss across all
# batches
loss = np.average(epochLoss)
losses.append(loss)
# check to see if an update should be displayed
if epoch == 0 or (epoch + 1) % 5 == 0:
print("[INFO] epoch={}, loss={:.7f}".format(int(epoch + 1),
loss))
Evaluating our classifier is done in the same way as in vanilla gradient descent — simply call predict on the testX data using our learned W weight matrix:
# evaluate our model
print("[INFO] evaluating...")
preds = predict(testX, W)
print(classification_report(testY, preds))
We’ll end our script by plotting the testing classification data along with the loss per epoch:
# plot the (testing) classification data
plt.style.use("ggplot")
plt.figure()
plt.title("Data")
plt.scatter(testX[:, 0], testX[:, 1], marker="o", c=testY[:, 0], s=30)
# construct a figure that plots the loss over time
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, args["epochs"]), losses)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
plt.show()
SGD Results
To visualize the results from our implementation, just execute the following command:
$ python sgd.py
[INFO] training...
[INFO] epoch=1, loss=0.1317637
[INFO] epoch=5, loss=0.0162487
[INFO] epoch=10, loss=0.0112798
[INFO] epoch=15, loss=0.0100234
[INFO] epoch=20, loss=0.0094581
[INFO] epoch=25, loss=0.0091053
[INFO] epoch=30, loss=0.0088366
[INFO] epoch=35, loss=0.0086082
[INFO] epoch=40, loss=0.0084031
[INFO] epoch=45, loss=0.0082138
[INFO] epoch=50, loss=0.0080364
[INFO] epoch=55, loss=0.0078690
[INFO] epoch=60, loss=0.0077102
[INFO] epoch=65, loss=0.0075593
[INFO] epoch=70, loss=0.0074153
[INFO] epoch=75, loss=0.0072779
[INFO] epoch=80, loss=0.0071465
[INFO] epoch=85, loss=0.0070207
[INFO] epoch=90, loss=0.0069001
[INFO] epoch=95, loss=0.0067843
[INFO] epoch=100, loss=0.0066731
[INFO] evaluating...
precision recall f1-score support
0 1.00 1.00 1.00 250
1 1.00 1.00 1.00 250
avg / total 1.00 1.00 1.00 500
The SGD example uses a learning rate of (0.1) and the same number of epochs (100) as vanilla gradient descent. The results of which can be seen in Figure 1.
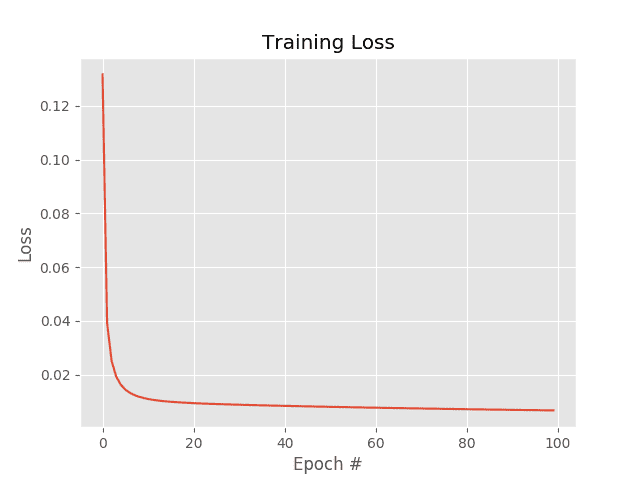
Investigating the actual loss values at the end of the 100th epoch, you’ll notice that loss obtained by SGD is nearly two orders of magnitude lower than vanilla gradient descent (0.006 vs 0.447, respectively). This difference is due to the multiple weight updates per epoch, giving our model more chances to learn from the updates made to the weight matrix. This effect is even more pronounced on large datasets, such as ImageNet, where we have millions of training examples and small, incremental updates in our parameters can lead to a low loss (but not necessarily optimal) solution.
What's next? We recommend PyImageSearch University.
84 total classes • 114+ hours of on-demand code walkthrough videos • Last updated: February 2024
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you'll find:
- ✓ 84 courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 84 Certificates of Completion
- ✓ 114+ hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 536+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!

