Image inpainting with OpenCV and Python

In this tutorial, you will learn how to perform image inpainting with OpenCV and Python.

Image inpainting is a form of image conservation and image restoration, dating back to the 1700s when Pietro Edwards, director of the Restoration of the Public Pictures in Venice, Italy, applied this scientific methodology to restore and conserve famous works (source).

Technology has advanced image painting significantly, allowing us to:

• Restore old, degraded photos
• Repair photos with missing areas due to damage and aging
• Mask out and remove particular objects from an image (and do so in an aesthetically pleasing way)

Today, we’ll be looking at two image inpainting algorithms that OpenCV ships “out-of-the-box.”

To learn how to perform image inpainting with OpenCV and Python, just keep reading!

Image inpainting with OpenCV and Python

In the first part of this tutorial, you’ll learn about OpenCV’s inpainting algorithms.

From there, we’ll implement an inpainting demo using OpenCV’s built-in algorithms, and then apply inpainting to a set of images.

Finally, we’ll review the results and discuss the next steps.

I’ll also be upfront and say that this tutorial is an introduction to inpainting including its basics, how it works, and what kind of results we can expect.

While this tutorial doesn’t necessarily “break new ground” in terms of inpainting results, it is an essential prerequisite to future tutorials because:

1. It shows you how to use inpainting with OpenCV
2. It provides you with a baseline that we can improve on
3. It shows some of the manual input required by traditional inpainting algorithms, which deep learning methods can now automate

OpenCV’s inpainting algorithms

To quote the OpenCV documentation, the Telea method:

… is based on Fast Marching Method. Consider a region in the image to be inpainted. Algorithm starts from the boundary of this region and goes inside the region gradually filling everything in the boundary first. It takes a small neighbourhood around the pixel on the neighbourhood to be inpainted. This pixel is replaced by normalized weighted sum of all the known pixels in the neighbourhood. Selection of the weights is an important matter. More weightage is given to those pixels lying near to the point, near to the normal of the boundary and those lying on the boundary contours. Once a pixel is inpainted, it moves to next nearest pixel using Fast Marching Method. FMM ensures those pixels near the known pixels are inpainted first, so that it just works like a manual heuristic operation.

The second method, Navier-Stokes, is based on fluid dynamics.

Again, quoting the OpenCV documentation:

This algorithm is based on fluid dynamics and utilizes partial differential equations. Basic principle is heurisitic [sic]. It first travels along the edges from known regions to unknown regions (because edges are meant to be continuous). It continues isophotes (lines joining points with same intensity, just like contours joins points with same elevation) while matching gradient vectors at the boundary of the inpainting region. For this, some methods from fluid dynamics are used. Once they are obtained, color is filled to reduce minimum variance in that area.

In the rest of this tutorial you will learn how to apply both the cv2.INPAINT_TELEA and cv2.INPAINT_NS methods using OpenCV.

How does inpainting work with OpenCV?

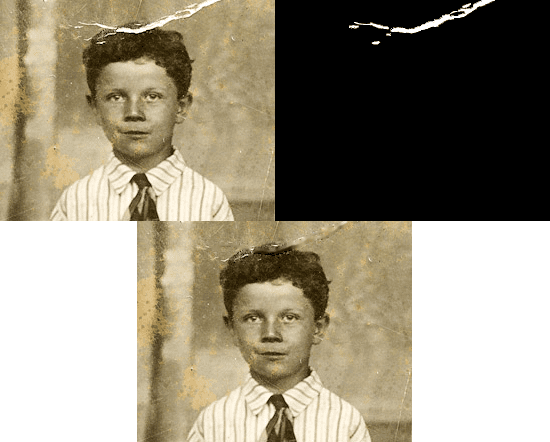
When applying inpainting with OpenCV, we need to provide two images:

1. The input image we wish to inpaint and restore. Presumably, this image is “damaged” in some manner, and we need to apply inpainting algorithms to fix it
2. The mask image, which indicates where in the image the damage is. This image should have the same spatial dimensions (width and height) as the input image. Non-zero pixels correspond to areas that should be inpainted (i.e., fixed), while zero pixels are considered “normal” and do not need inpainting

An example of these images can be seen in Figure 2 above.

The image on the left is our original input image. Notice how this image is old, faded, and damaged/ripped.

The image on the right is our mask image. Notice how white pixels in the mask mark where the damage is in the input image (left).

Finally, on the bottom, we have our output image after applying inpainting with OpenCV. Our old, faded, damaged image has now been partially restored.

How do we create the mask for inpainting with OpenCV?

At this point, the big question is:

“Adrian, how did you create the mask? Was that created programmatically? Or did you manually create it?”

For Figure 2 above (in the previous section), I had to manually create the mask. To do so, I opened up Photoshop (GIMP or another photo editing/manipulation tool would work just as well), and then used the Magic Wand tool and manual selection tool to select the damaged areas of the image.

I then flood-filled the selection area with white, left the background as black, and saved the mask to disk.

Doing so was a manual, tedious process — you may be able to programmatically define masks for your own images using image processing techniques such as thresholding, edge detection, and contours to mark damaged reasons, but realistically, there will likely be some sort of manual intervention.

The manual intervention is one of the primary limitations of using OpenCV’s built-in inpainting algorithms.

I discuss how we can improve upon OpenCV’s inpainting algorithms, including deep learning-based methods, in the “How can we improve OpenCV inpainting results?” section later in this tutorial.

Project structure

Scroll to the “Downloads” section of this tutorial and grab the .zip containing our code and images. The files are organized as follows:

$ tree --dirsfirst
.
├── examples
│   ├── example01.png
│   ├── example02.png
│   ├── example03.png
│   ├── mask01.png
│   ├── mask02.png
│   └── mask03.png
└── opencv_inpainting.py

1 directory, 7 files

Implementing inpainting with OpenCV and Python

# import the necessary packages
import argparse
import cv2

# construct the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-i", "--image", type=str, required=True,
	help="path input image on which we'll perform inpainting")
ap.add_argument("-m", "--mask", type=str, required=True,
	help="path input mask which corresponds to damaged areas")
ap.add_argument("-a", "--method", type=str, default="telea",
	choices=["telea", "ns"],
	help="inpainting algorithm to use")
ap.add_argument("-r", "--radius", type=int, default=3,
	help="inpainting radius")
args = vars(ap.parse_args())

# initialize the inpainting algorithm to be the Telea et al. method
flags = cv2.INPAINT_TELEA

# check to see if we should be using the Navier-Stokes (i.e., Bertalmio
# et al.) method for inpainting
if args["method"] == "ns":
	flags = cv2.INPAINT_NS

# load the (1) input image (i.e., the image we're going to perform
# inpainting on) and (2) the  mask which should have the same input
# dimensions as the input image -- zero pixels correspond to areas
# that *will not* be inpainted while non-zero pixels correspond to
# "damaged" areas that inpainting will try to correct
image = cv2.imread(args["image"])
mask = cv2.imread(args["mask"])
mask = cv2.cvtColor(mask, cv2.COLOR_BGR2GRAY)

# perform inpainting using OpenCV
output = cv2.inpaint(image, mask, args["radius"], flags=flags)

# show the original input image, mask, and output image after
# applying inpainting
cv2.imshow("Image", image)
cv2.imshow("Mask", mask)
cv2.imshow("Output", output)
cv2.waitKey(0)

We display three images on-screen: (1) our original damaged photograph, (2) our mask which highlights the damaged areas, and (3) the inpainted (i.e., restored) output photograph. Each of these images will remain on your screen until any key is pressed while one of the GUI windows is in focus.

OpenCV inpainting results

We are now ready to apply inpainting using OpenCV.

Make sure you have used the “Downloads” section of this tutorial to download the source code and example images.

From there, open a terminal, and execute the following command:

$ python opencv_inpainting.py --image examples/example01.png \
	--mask examples/mask01.png

On the left, you can see the original input image of my dog Janie, sporting an ultra punk/ska jean jacket.

I have purposely added the text “Adrian wuz here” to the image, the mask of which is shown in the middle.

$ python opencv_inpainting.py --image examples/example02.png \
	--mask examples/mask02.png --method ns

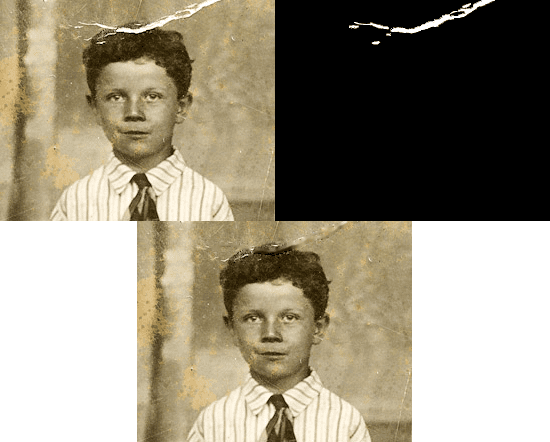
On the top, you can see an old photograph, which has been damaged. I then manually created a mask for the damaged areas on the right (using Photoshop as explained in the “How do we create the mask for inpainting with OpenCV?” section).

The bottom shows the output of the Navier-Stokes inpainting method. By applying this method of OpenCV inpainting, we have been able to partially repair the old, damaged photo.

Let’s try one final image:

$ python opencv_inpainting.py --image examples/example03.png \
	--mask examples/mask03.png

On the left, we have the original image, while on the right, we have the corresponding mask.

Notice that the mask has two areas that we’ll be trying to “repair”:

1. The watermark on the bottom-right
2. The circular area corresponds to one of the trees

In this example, we’re treating OpenCV inpainting as a method of removing objects from an image, the results of which can be seen on the bottom.

Unfortunately, results are not as good as we would have hoped for. The tree we wish to have removed appears as a circular blur, while the watermark is blurry as well.

That begs the question — what can we do to improve our results?

How can we improve OpenCV inpainting results?

One of the biggest problems with OpenCV’s built-in inpainting algorithms is that they require manual intervention, meaning that we have to manually supply the masked region we wish to fix and restore.

Manually supplying the mask is tedious — isn’t there a better way?

In fact, there is.

Using deep learning-based approaches, including fully-convolutional neural networks and Generative Adversarial Networks (GANs), we can “learn to inpaint.”

These networks:

• Require zero manual intervention
• Can generate their own training data
• Generate results that are more aesthetically pleasing than traditional computer vision inpainting algorithms

Deep learning-based inpainting algorithms are outside the scope of this tutorial but will be covered in a future blog post.

Summary

These methods are traditional computer vision algorithms and do not rely on deep learning, making them easy and efficient to utilize.

However, while these algorithms are easy to use (since they are baked into OpenCV), they leave a lot to be desired in terms of accuracy.

Not to mention, having to manually supply the mask image, marking the damaged areas of the original photograph, is quite tedious.

In a future tutorial, we’ll look at deep learning-based inpainting algorithms — these methods require more computation and are a bit harder to code, but ultimately lead to better results (plus, there’s no mask image requirement).

To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), just enter your email address in the form below!